Teste - 2º Ano - 1º Semestre

Amostras Aleatórias Simples

Estamos de volta.

Vamos começar por tratar das Amostras Aleatórias Simples.

Teste 2

Exercicio - Segundo Teste

Primeiro Teste

Teste Modelo - 29 de Abril

IDH (HDI)

Abaixo apresentam-se alguns exemplos de correlação forte:

Rendimento percapita com indice de rendimento percapita 0,9735
Rácio combinado para a educação com o indice de educação 0,8531
Indice de desenvolvimento humano com o indice de rendimento percapita 0,9532
Indice de desenvolvimento humano com o indice de esperança de vida 0,8307

Alguns exemplos de correlação fraca:

Rácio de literacia nos adultos com o rendimento percapita -0,3559
Rácio de literacia nos adultos com o indice de esperança de vida -0,0812
Esperança de vida à nascença com rácio de literacia nos Adultos -0,0517
Rácio de literacia nos adultos com rácio combinado para a educação 0,2652

O facto de terem sido seleccionados apenas 70 países, deriva destes pertencerem ao grupo com maoir indice de desenvolvimento humano e, como tal, apresentarem valores mais homogéneos.

São igualmente estes os países em que a economia formal é mais representativa e consequentemente onde a informação económica disponível é mais fidedigna.

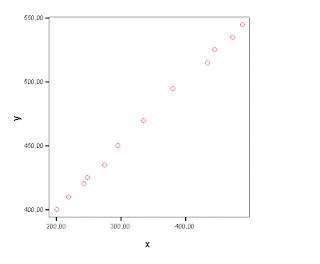
Coeficiente de Correlação de Pearson - r

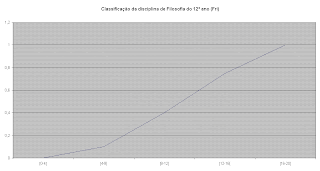
Foram seleccionados apenas 100 registos de cada disciplina pelo facto da sua representação gráfica ser mais simples.




O facto da disciplina de Bilologia ser aquela que apresenta um coeficiente de corelação mais elevado, pode prender-se com o facto da disciplina ser uma das nucleares para o acesso a cursos superiores em que as médias de «entrada» são mais elevadas (ie: Medicina, Veterinária, Enfermagem, etc). Assim os professores podem de alguma forma «inflacionar» as notas finais para de alguma forma ajudarem os alunos, situação que não se verifica nas notas de exame.

Coeficiente de Assimetria e Achatamento

Ranking de Escolas

Com base na informação acima apresentada, pode constatar-se que todas as seguintes afirmações são VERDADEIRAS:


1) média CE é menor que a média CIF em todas as disciplinas
2) desvio padrão das CE é maior que o desvio padrão das CIF em todas as disciplinas
3) médias CE são mais baixas no grupo Matemática e Ciências que em Português e Literárias
4) desvios padrão dos CE são maiores no grupo Matemática e Ciências que em Português e Literárias
5) diferença média CIF – média CE é maior no grupo Matemática e Ciências que em Português e Literárias

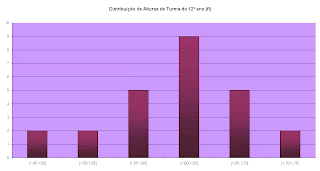
Distribuição Normal

Como se pode verificar a distribuição normal poderá aplicar-se a diversas áreas da acção humana.

A noticia abaixo apresenta um ranking dos jornais online mais lido pelos internautas.

Neste caso temos o jornal mais lido e o menos lido, sendo que entre um e outro temos mais publicações:

«Em termos de utilizadores únicos, Maisfutebol ocupa a quinta posição, com 309 mil leitores. O top 5 é composto da seguinte forma: «A Bola» (426), «Record» (413), «Público» (378) e «Sapo Notícias» (365).»

http://www.maisfutebol.iol.pt/noticia.php?div_id=1480&id=901941

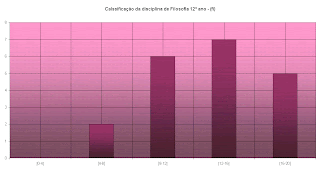
Outra situação que permite ser retratada através da distribuição normal é a muito falada classificação das escolas em termos de ranking:

«As melhores e as piores secundárias do país em 2006
Os melhores resultados nos exames nacionais do 12º ano encontram-se este ano mais uma vez no Porto – e, mais uma vez, numa escola privada: o Grande Colégio Universal. A pior escola secundária fica em Vilar Formoso.»

http://sic.sapo.pt/online/noticias/vida/especiais/ranking+escolas+2006/20061022+Ranking+das+Escolas.htm

Média e Desvio Padrão - Efeitos da Adição e da Multiplicação de uma constante

Pode concluir-se que ao somar 2 valores a cada aluno, sobe o valoor da média e mantém o do desvio padrão.

Ao multiplicarem-se os valores de cada aluno por 3, tanto a média como o desvio padrão evoluem na mesma proporção, ou seja, aumentam o seu valor 3 vezes.

Medidas de Dispersão - Exercicio 3

Medidas de Dispersão - Exercicio 2

Funções Excel

Medidas de Dispersão - Exercicio 1

Teste

Quartis

Revisões

Revisões

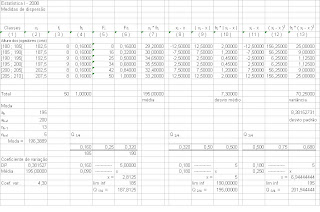
Critica dos Dados

Previamente à publicação de dados estatisticos é necessário proceder à sua critica de forma a evitar erros que possam, consequentemente, influenciar de forma errada as análises que se venham a fazer com base nesses mesmos dados.

Assim, é fundamental suprimir valores estranhos que influam nos resultados finais.

Cálcular a Mediana

A Mediana é sempre o valor central da frequência caso esta seja impar.

Como tal o valor da Medidana na seguinte frequência:

10, 11, 12, 12, 12, 13, 14, 14, 15, 15, 17

é o 13.

Calcular a Moda

A moda é o valor que mais se repete.

Assim, tendo em consideração os seguintes valores:

10, 11, 12, 12, 12, 13, 14, 14, 15, 15, 17

Pode dizer-se que a Moda é 12.

Cálcular a Média

Tendo em consideração os eguintes valores:

10, 11, 17, 15, 14, 13, 12, 12, 12, 14, 15

A média calcula-se somando todos os valores e dividindo pelo número de parcelas

10+11+17+15+14+13+12+12+12+14+15=145/11=13.1

Média = 13.1 (13).